Механические воздействия и их характеристики

При эксплуатации и транспортировке РЭСИ подвергаются механическим воздействиям: вибрационным, ударным и линейным нагрузкам, а также звуковому давлению (акустическим шумам). К изделиям, предназначенным для функционирования в условиях воздействия механических нагрузок, предъявляют требования по прочности и устойчивости при воздействии этих нагрузок. К изделиям, не предназначенным для функционирования в условиях воздействия механических нагрузок, предъявляют требования только по прочности при воздействии этих нагрузок. Уровни вибрационных воздействий показаны на рисунке 1.4.

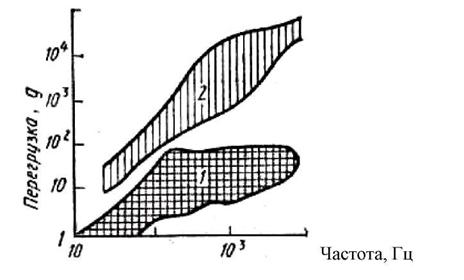
Рисунок 3 — Уровни вибрационных воздействий, которым подвергаются РЭСИ:

1 — вибрация; 2 — вибрация, возбуждаемая ударом

Вибрация — один из самых опасных и наиболее часто встречающихся на практике видов механических воздействий. В общем случае под вибрацией понимают, колебания самого изделия или каких-либо частей его конструкции. Вибрации приводят к поломкам конструкции, обрывам проводов и кабелей, нарушению герметичности, к механическим напряжениям и деформациям в РЭСИ. Наиболее часто вибрационные нагрузки возникают на самолетах и ракетах.

Механическая прочность, необходимая для нормального функционирования РЭСИ во время и после воздействия на них различных вибрационных нагрузок, должна быть заложена на этапе проектирования изделий. Для этого РЭСИ рассматривают как механические системы и применяют аналитические методы расчета их механических характеристик.

Далее приведен простой пример, когда изделие может быть представлено в виде механической колебательной системы с одной степенью свободы (рисунок 4)

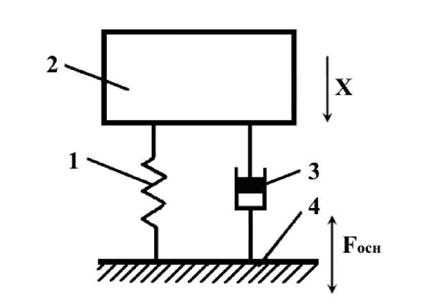
Рисунок 4 — Схема линейного осцилятора с вязким трением:

1—пружина; 2—груз; 3— демпфер; 4 — стол вибростенда

Система состоит из груза массой m, пружины с жесткостью С и демпфера вязкого трения с коэффициентом демпфирования ŋ. Движение массы m от определяется изменением только одной координаты х под действием возбуждающей силы Fосн. Уравнение движения системы может быть получено на основе принципа Даламбера, согласно которому в каждый момент времени все силы, действующие на систему, находятся в равновесии, если в их число входит сила инерции. В общем случае дифференциальные уравнения движения любой колебательной механической системы могут быть составлены на основе уравнения Лагранжа в обобщенных координатах. На систему, изображенную на рисунке 4, действуют:

1) возбуждающая сила, приводящая к колебаниям опорного основания (например, стола вибростенда) с частотой со и амплитудой А;

Fосн=Asin(ωt),(6)

2)сила инерции Тx2 (х2 — ускорение); сила вязкого демпфирования ŋx1 (х1—скорость), пропорциональная мгновенной скорости массы и направленная в сторону, противоположную этой скорости;

3)сила упругости пружины Сх (х — координата центра масс груза). Уравнение движения массы m от относительно положения статического

равновесия имеет вид:

mx2+ŋx+Сx= A∙sin∙ωt.(7)

Разделив правую и левую части уравнения (1.3) на m после преобразования получим:

Х2+2∙δо∙ωо∙x+ ω2оx=ω2о∙XCT∙sin(ωt),(8)

где δо = ŋ/(2 ) — параметр, пропорциональный коэффициенту демпфирования;

ω=—угловая частота собственных недемпфированных колебаний системы;

Хст=A/С — удлинение пружины, которое она получила бы под действием статической силы, равной амплитуде Л возбуждающей силы.

Решение уравнения (1.4) может быть представлено в виде суммы свободных и вынужденных колебаний:

(9)

где φ0 и φ — начальные фазы

(0)

μ — коэффициент динамичности, показывающий, во сколько раз амплитуда вынужденных колебаний при действии возбуждающей силы вида (2) больше статического отклонения пружины;

v=ω/ω0 - безразмерный параметр, пропорциональный частоте возбуждающей силы.

Из первого слагаемого уравнения (5), представляющего выражение для свободных колебаний системы при наличии демпфирования, видно, что даже при малом значении δо множитель с течением времени t стремится к нулю и, следовательно, свободные колебания затухают.

Установившиеся вынужденные колебания определяются вторым слагаемым (5). Особенность этих колебаний состоит в том, что их амплитуда зависит не только от параметров системы и возбуждающей силы, но от частоты

со. При v= коэффициент динамичности максимален:

Copyright © 2024 - All Rights Reserved - www.chemicalnow.ru