5. Процессы. Второй закон термодинамики
δA′ max= (U1 – TS1 + PV1) – (U2 – TS2 + PV2) = G1 – G2 = – ΔG,
U – TS + pV = G,
A′ max= – ΔG.
Работа изобарно-изотермического процесса равна убыли изобарно-изотермического потенциала – физический смысл этой функции;
2) функция – полный дифференциал, однозначна, конечна, непрерывна.
G = U – TS + pV,
dG = dU – TdS – SdT + pdv + vdp,
dG = TdS – pdV – TdS – SdT + pdv + vdp,
dG = –SdT + Vdp,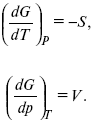 
Повышение температуры приводит к тому, что изобарно-изотермический потенциал уменьшается, так как перед S стоит знак «минус». Повышение давления приводит к тому, что изобарно-изотермический потенциал увеличивается, так как перед V стоит знак «плюс»;
3) G как критерий направленности процесса в изолированной системе.
Для самопроизвольного процесса: (ΔG )P,T < 0. Для несамопроизвольного процесса: (ΔG )P,T > 0. Для равновесного процесса: ( ΔG)P,T = 0
ΔG(P,T)≤ 0.
Изобарно-изотермический потенциал в самопроизвольных процессах уменьшается, и, когда он достигает своего минимума, то наступает состояние равновесия.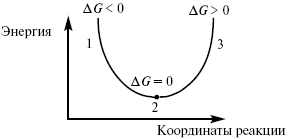 
Рис. 5
где 1 – самопроизвольный процесс;
2 – равновесный процесс;
3 – несамопроизвольный процесс.
Совершается работа за счет ΔU и ΔH .
Противодействующие факторы.
Энтальпийный фактор характеризует силу притяжения молекул. Энтропийный фактор характеризует стремление к разъединению молекул.
Энтальпия – Н Внутренняя энергия – U.
H = U + PV,
dH = dU + pdv + vdp,
U = TS – PV,
dU = TdS – SdT + pdV + Vdp,
dH = –pdV + pdV + Vdp; U = TdS + VdP.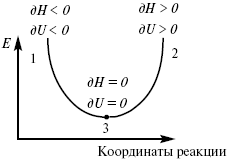 
Рис. 6
где 1 – самопроизвольный процесс,
2 – несамопроизвольный процесс,
3 – равновесный процесс,
(dH)P,T ≤ 0,
(dU)S,T ≤ 0.
Уравнения Гиббса – Гельмгольца – уравнения максимальной работы
.
Они позволяют установить связь между максимальной работой равновесного процесса и теплотой неравновесного процесса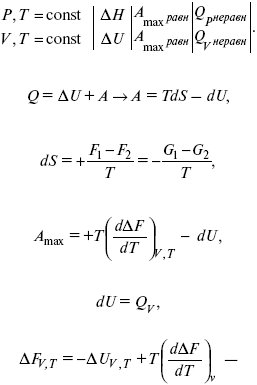 
уравнение Гельмгольца (уравнение связывающее функции F и G с их температурными производными). 
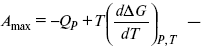
уравнение Гиббса (уравнение связывающее функции F и G с их температурными производными).
Уравнения эти дают возможность рассчитать работу через температурный коэффициент функции Гельмгольца или через температурный коэффициент функции Гиббса.
Уравнение Клаузиуса-Клапейрона
Оно позволяет применить второй закон термодинамики к фазовым переходам. Если рассчитать процессы, в которых совершается только работа расширения, то тогда изменение внутренней энергии
U2 – U1 = T(S2 – S1) – P(V2 – V1),
(U1 – TS1 + PV1) = (U2 – TS2 + PV2),
G1 = G2 – в условиях равновесия.
Предположим, что 1 моль вещества переходит из первой фазы во вторую.
I фаза =>
dG1 = V1dp – S1dT.
II фаза =>
dG2= V2dp – S2dT, при равновесии dG2 – dG1 = 0
dG2 – dG1 = dp(V2 – V1) – dT(S2 – S1) –
нет условного равновесия,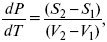 
где dP/dT – температурный коэффициент давления,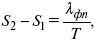 
где λ фп – теплота фазового перехода.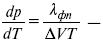 
Смотрите также
Химия отрасли
Важнейшим
элементом в решении задачи выпуска продукции высокого качества является
технохимический контроль производства, заключающийся в проверке исходного сырья
и материалов при поступлени ...
Технология неконцентрированной азотной кислоты
Азотная
кислота по объему производства занимает среди других кислот второе место после
серной кислоты. Все возрастающий объем производства HNO3
объясняется огромным значением азотной кислот ...